Multispectral optoelectronic systems.
TARASOV Viktor Vasilievich, Doctor of Technical Sciences
YAKUSHENKOV Yuri Grigorievich, Doctor of Technical Sciences
In this article, after considering some terminological issues, an attempt is made to assess the feasibility of using optical spectral methods in solving the most important problem facing many optoelectronic systems, namely, isolating a useful signal from a background of interference.
Recently, in foreign and, what is especially regrettable, in domestic scientific and technical publications and documents, there have been more frequent cases of using terms whose meaning is distorted by the authors of these publications, or perhaps is simply not clear to them.
Sometimes this is connected with unjustified and illegal borrowing of individual words and phrases from foreign languages, for example, the term “hyperspectral” contradicts the norms of the Russian language (it is something like “gimer-maslyanogo oil”) and physical meaning (there may be terms “hypersonic”, equivalent to “supersonic”, and “hyperresolution”, etc., but what is “hyperspectral” if the spectrum is a physical and mathematical concept, and not a quantitative indicator?).
Therefore, in order to reasonably use the widely used term “intelligent” (“intelligent robot”, “intelligent system”, “intelligent weapon”, etc.), it is worth remembering that the concept “intelligence consists of many components inherent in highly organized subjects of living nature, higher animals and humans, and therefore when using the term “intelligent optical-electronic system” or intelligent weapon”, it is necessary to agree on what properties and features of the intelligence of higher animals and humans are used in this system or weapon.
The use of human intelligence created by millennia of evolution often comes down to such processing of information about the surrounding world or some properties of certain objects, when consciously or unconsciously from the entire volume of information the most essential properties (signs) of a phenomenon or object for solving a specific problem are selected.
Human intelligence often allows such information processing to be performed in the most rational way, although not always optimally. Technical means that perform such processing or work in close cooperation with a human operator can be called intelligent. These include, first of all, optical and optoelectronic systems, if only because 80-95% of information about the surrounding world is received by living beings, including humans, through the visual apparatus [1].
The rapid development of optoelectronic systems (OES), which has been ongoing for several decades, allows for the continuous expansion of their range of applications and the solution of many complex problems, in particular, those that were not so long ago available to automatic systems.
The development paths of the OES of technical vision largely coincide with what nature has created in the form of the visual apparatus of higher animals and humans.
Thus, it is believed that this visual apparatus interacts with the brain in two ways: by transmitting an image for comparing it with standards of known images (analog — optical-electronic correlators) or for analyzing the image according to a number of primary features (analog — OES with spectral optical, spatial-frequency and spatial-temporal filtration).
In the last decade, numerous developments of OES based on bionic (biocybernetic) principles have been carried out.
Research of these principles and creation of the element base for their practical implementation is, perhaps, the main trend in the development of modern optical-electronic instrumentation.
The systems being developed often use several parallel channels for receiving and primary processing of information, multi-element radiation receivers, complex signal processing algorithms based on specialized logical and computing devices.
Increasing attention is being paid to adaptive optical-electronic devices that implement feedback at the parametric and circuit level to control sensitivity, the magnitude of angular fields, the parameters of optical spectral, spatial and time-frequency filters, as well as other characteristics of the OES.
Here, too, biocybernetic principles used in living nature are widely used.
The analysis of individual components of intelligence related to the visual apparatus of higher animals and humans has been repeatedly carried out in the literature.
We can briefly recall some essential features of the visual apparatus of higher animals and humans, important from the point of view of their reproduction in the OES of technical vision, serving to detect, recognize and classify various objects.
Psychophysiologists have observed that when recognizing images, humans primarily use the principle of preference for certain features.
For this purpose, they compare objects of the same class, highlighting their commonality and selecting dividing features.
A feature of psychophysiological processes of perception of visual (optical) information in higher animals and humans is decorrelation of images in space and time in order to eliminate statistical redundant connections of adjacent image elements and successive frames already in the primary information processing system.
This allows using only the most informative features of recognizable images and most economically encoding information for transmission to the secondary processing system — the brain.
The visual organs of most lower animals do not have the ability to distinguish the color of objects and work in a relatively narrow spectral range.
An exception are some species of snakes, such as the American rattlesnake, which has a “thermal vision” apparatus with about 1000 sensitive elements and a temperature resolution of t = 10-3 °C.
The human retina contains three types of cones with different spectral characteristics (R, G, B).
Adaptation of each of these types to changes in illumination occurs independently of each other.
At the output of the so-called bipolar cells, signals from cones with different spectral characteristics sr, sg and sb are converted into a total achromatic and two color difference signals:
SZ = SR +SG + SB,
SRG = CGSG – CRSR,
SRGB = GRSR + CGSG – CBSB,
where SR, CG and CB are weighting coefficients [2].
Due to the linearity of signal transformation, determined by the change in the illumination of the cones and proportional to the ratio of the increment of the effective illumination of the cone to its average value, i.e. contrast, the perception of the color tone and saturation of the image does not depend on the brightness of the observed object [2].
The human visual apparatus has the property of color constancy, i.e. the ability to correctly recognize different colors regardless of the spectral composition of the light source [2].
Other features of the visual apparatus of intelligent beings are the adaptive “exchange” of the sensitivity of the elements of the retina for resolution (with an increase in the illumination of the image) due to the accumulation of the signal, as well as the use of eye movements (regular and random — tremor), which allows information to be compressed up to 106 times and transmit to the brain only information about changes in the features of the image [1].
The most frequently used interpretation of recognition is geometric, in which n features of a signal (image) form a feature vector in an n-dimensional space, i.e. points or clusters (sets of randomly distributed points) that characterize individual objects or their images.
The assignment of these points or clusters to a particular object (class of objects) is carried out using discriminant (separating) functions [3, 4].
Each class of images (type of targets) has its own vector of mathematical expectation and covariance matrix, taking into account the random nature of the signal features.
For the formation of an n-dimensional feature vector, a theoretically minimal number of training images (standards) equal to n + 1 is required. (Sometimes in practice, with reliable recognition of particularly complex images, the required number of training images can reach 10n and even 100n[3]).
Due to the random nature of the features characterizing the most diverse objects (classes of objects) and signals arriving at the input of the recognition system (RSI), many applied problems, especially in the field of military equipment, require a statistical approach to solving the problems of detection, recognition, and classification.
The methods of statistical pattern recognition using the probability distribution functions of features and classes of patterns have been studied quite well and theoretically seem to be the most promising for RSI of an intelligent type for various purposes [1, 3, 4, 5, etc.].
The form of presentation of the class of recognizable objects can determine the type of algorithm for processing information obtained at the output of the primary information processing system of the OES.
Thus, if a class of objects is represented by a deterministic spectral feature or a feature obtained by averaging a large number of spectra (1st order statistics), then the information processing algorithms can be quite simple, for example, the determination of spectral ratios (ratios of signals falling on individual spectral working ranges) can be carried out by quantization by level or by using linear discriminant functions.
In recent decades, algorithms have come to be used that are based on comparing known distributions of feature sets in an n-dimensional space with a distribution corresponding to changes in features in a real system (2nd order statistics).
The discriminant functions in this case are 2nd order curves.
Processing of features in recognition systems is most often carried out in three ways: selection of the most informative features (selection of subsets), formation of relationships of individual features (relationships of individual components of the feature vector), and formation of linear combinations of individual features.
All these methods are simple enough for practical implementation. In recognition theory, the term “essential dimensionality” is sometimes used, denoting the minimum number of dimensions (distinguished features) necessary for an accurate representation of sets of data on the recognized object.
Due to the frequent need in practice to process very large volumes of optical” information in real time, the use of the most mastered digital computers of sequential action is not always sufficiently effective.
This is, for example, true when implementing methods for extracting (detecting, recognizing) complex images observed on non-uniform (“variegated”) backgrounds. Adaptive OES with blocks for generating invariant informative features based on neural networks are already known today [6].
To solve the problems of detecting optical signals and images, for example, an image of an object that is quite complex in shape, spectrum and other features, located on a complex “variegated” background, modern OES almost universally use such a description of images (a set of processed signals), which contains only a limited number of distinctive features.
The selection of features that most significantly distinguish a given class of images (objects, images, signals) is the most important task in the development of OES operating as part of an intelligent weapon.
Therefore, when developing new and improving existing OES, it is very important to select the minimum number of such features that provide the specified performance indicators of the OES, but do not complicate their design and thereby do not reduce the reliability of the systems and increase the cost of their production and operation.
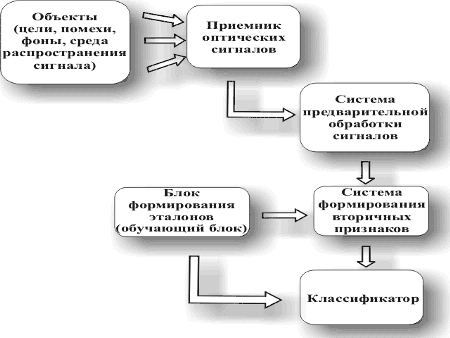
Figure 1 shows a structural diagram of the automatic recognition system of optical images (signals).
The receiver of optical signals is understood to be a combination of an optical system and a photodetector, i.e. a primary information processing system [4].
Fig. 1. Structural diagram of the system
for automatic recognition of optical images
The most frequently used groups of features are:
— geometric, the selection and processing of which depends primarily on the spatial resolution of the OES; these features include the size and shape of the image; histograms of the distributions of angles, chords, side lengths; geometric moments; Fourier and Mellin spatial-frequency spectra; Walsh functions, etc.;
— spectral, the selection and processing of which depends on the spectral resolution of the OES; these include absorption, emissivity and reflectivity; color, etc.;
— energy, usually characterized by the signal-to-noise ratio;
— dynamic, using information about changes in the coordinates of an object, the speed of its movement, etc.
In each specific case of detection, recognition and classification of certain objects, it is advisable to use limited sets of stable features in order not to complicate the design of the OES.
In the literature, a three-dimensional array of information is most often considered, i.e. in most developments and attempts to create intelligent” OES, a set of geometric-optical and dynamic features of objects (spatial and spatio-temporal filtering of signals against the background of interference) is used.
The primary features used are the parameters of a two-dimensional image: coordinates in the image plane, image dimensions, image shape, geometric moments, etc., and one temporal feature, for example, the speed of image movement, signal duration, etc.
The spatial resolution of the OES is determined by the parameters and characteristics of the optical system, which determine the quality of the image it creates, as well as the parameters of the radiation receiver (for example, the step of a multi-element receiver) and the selected algorithm for generating and processing the signal taken from the receiver.
Spectral optical features of objects and signals are used in most cases in a limited way — by using simple rejection (band, single-band) or two-color (two-band) spectral optical filtering. Very little is known about the use of balanced spectral filtering [4].
At the same time, increasing the number of spectral channels (working spectral ranges) in the OES to at least two or three, as is the case in the human visual apparatus (see above), can significantly increase the intelligence of these systems and the complexes they are part of, i.e. improve their quality indicators.
For example, as reported in [7], the simultaneous use of two spectral ranges (3-5 and 8-13 µm) in an OES designed to detect and recognize tank-type targets against a motley background significantly increases the probability of correct target detection (by 5-7%), compared to the same probability provided by using only spatial features in combination with signal processing in a neural network.
Changes in the characteristics of an object and the background against which the object is observed, changes in the conditions for receiving signals from objects, the occurrence of additional interference, and finally, changes in the parameters and characteristics of the recognition system itself (RSU) – these are the factors that, before others, make it advisable to select and form such primary and secondary signal characteristics that will be most stable (invariant) to the indicated changes.
Unfortunately, most literature on optical image recognition mainly considers the stability of spatial and spatiotemporal features of objects and optical signals, but not the spectral optical characteristics of the radiation of objects and the signals corresponding to them.
At the same time, it was noted that such a “geometric approach turned out to be productive only in the simplest tasks, for example, in recognizing standard fonts and images, and in recognizing natural scenes it is clearly untenable [1].
It can be noted that some geometric optical features of objects and their images subject to recognition have bimodal and even multimodal probability distribution functions, having not one, but two or more maxima.
At the same time, the spectral reflective and emissive abilities of most objects of natural or artificial origin (targets, interference, backgrounds) are described by a single-modal probability distribution function, most often Gaussian (normal).
This significantly simplifies the process of training the classifier of the recognition system based on these features, i.e. spectral optical features may be preferable to geometric optical ones.
As an example of relatively stable features of optical signals, i.e. having a small spread within their cluster, we can indicate the spectrum of solar radiation, which determines the properties of the signal reflected from these objects; the emission spectra of many objects of natural and artificial origin close to black bodies (Planck functions); the reflectivity and emissivity of many materials and coatings used in the creation of artificial radiation sources (objects).
It is well known that one of the fairly stable and informative features of many objects is color.
The spectral resolution of the OES depends on the number of working spectral ranges or “spectral windows” of the system, in which data on the viewed field (“scene”) is collected. The question of the number of such windows required for reliable recognition is very important.
It is known from the theory of pattern recognition that with an increase in the number of spectral windows, i.e. with an increase in the so-called “complexity of measurements”, the accuracy of recognition increases only up to a certain point, and then, with a further increase in this number, it decreases [3].
This is explained by the fact that with an increase in the number of spectral ranges, it is necessary to estimate a set of statistics of an increasingly higher dimension based on a limited fixed number of spectral samples.
This significantly complicates the data processing system in a real system, for example, the machine time required to perform complex calculations increases unjustifiably. Thus, there is an optimal number of spectral features.
For example, in remote sensing of natural resources, it was found that the maximum probability of recognition by spectral features is achieved with three recognition features, and the probability of recognition when using a larger number of them, for example, 12 features, is significantly lower [3].
One of the directions for further development of multispectral OES recognition (“intelligent multispectral OES”) is the use of a number of spectral channels close to the essential dimension of the functions describing the spectral emissivity and reflectivity of detection and recognizable objects.
For example, in [3] it is stated that the essential dimensionality of multispectral data in the range of 0.4 — 15.0 µm, determined for the phenomena of reflection and emission of energy from the Earth's surface, is close to six.
When using spectral features inherent in most objects recognized in practice, it is important to use a high degree of correlation of these features, resulting from the physical nature of optical radiation and the determinism of the laws describing this nature, for example, Planck's law.
This corresponds to a large elongation of the cluster of n features in n-dimensional space, which can be used to obtain a feature vector in a space of lower dimensionality without significant loss of information.
This also leads to the conclusion that it is possible to reduce the number of spectral features used (spectral windows, spectral ratios) to three or four, and sometimes to two.
For example, it is known that the dimensionality of the vector of spectral features used in the operation of the Landsat-1 and Landsat-2 multispectral scanning systems was 4 (four spectral operating ranges), however, the greatest contrast of the details of the image of the earth's surface obtained with the help of these systems was achieved using only two windows [3].
The selection of a subset of spectral features is carried out by identifying such a working range of the OES operation in which the energy signal/noise ratio is maximum. The formation of the ratio of signals falling on two narrow spectral ranges is well known — two-color spectral optical filtration.
The above-described model of color perception by the human visual apparatus is, in fact, the implementation of the method of forming linear combinations of three monochromatic radiations («pure» colors).
The well-known method of balanced spectral filtering [4] can be considered as the formation of a linear combination (combinations) of signals generated in two or more relatively wide spectral ranges.
Less well-known systems are those in which the numerator and denominator of the spectral ratio are the sums or differences of signals received in two spectral ranges, which makes it possible to “subtract” or reduce” the signal generated by unwanted background radiation or interference.
This method can be classified as both a method of relations and a method of linear combinations.
Its implementation in military-purpose OES is of great practical interest.
Taking into account possible changes in the optical spectrum (the effective spectral emissivity of an object or the spectral density of the image illumination), associated, for example, with a change in the operating mode of power plants at the object, or with a change in the conditions of the optical signal along the “object – OES” route, or with a change in the conditions of irradiation of the object by natural extraneous sources, etc., it is advisable to have flexible standards of spectral features – spectral ratios.
In this case, the standard model becomes invariant with respect to random or deterministic variations of signal features within certain limits or ranges of change of the specified factors. The capabilities of modern digital holography allow the use of large sets of such non-generalized standards.
Of interest may be the distribution statistics (histograms) of primary features such as the extent or area of sections of the same color.
Energy resolution, defined as the number of resolved levels of object radiance or image illumination, is selected in accordance with the required signal-to-noise ratio.
It is well known that the probability of detection and recognition increases with the growth of this ratio. In this case, it is necessary to take into account the interrelation of spatial, spectral and energy resolution, which takes place in real OES.
For example, if high spatial resolution is achieved by reducing the size of an image element, then due to this, a smaller amount of energy will fall on this element, which is necessary for dividing it into spectral working ranges and obtaining the required signal-to-noise ratio in each of these ranges.
The main obstacles to the creation of “intelligent” multispectral OES are the well-known difficulties in creating relatively inexpensive, highly sensitive, wide-range (operating in a wide spectral range) photodetector devices (PDD) with high spatial, spectral and temporal resolution.
This also includes the difficulties in creating economical, durable, small-sized PD cooling systems and a number of other technical and economic problems.
The attempts to create such OES in the form of Fourier spectrometers or multichannel video spectrometers are not always successful, since, for example, the requirement to work in real time is not met, as well as a number of other requirements.
The problem of calibration and training of “intelligent” OES (self-training) in changing conditions of their operation and especially with instability of the parameters (features) of the observed objects and the signals generated by these objects remains very important.
When creating automatic OES recognition systems, it is advisable to provide for human participation not only at the stage of collecting information about various characteristics of objects and signals, but also in the process of training the classifier, which can significantly simplify this process.
The effectiveness of using multispectral OES largely depends on knowledge of the parameters and characteristics of the objects on which they work (target signatures, interference, backgrounds).
It is no coincidence that there is very little data on the signatures of military equipment in the open literature. In 1993, a special department was formed in the US Department of Defense Intelligence Agency to conduct reconnaissance and create a database of signatures of reconnaissance targets (Measurements and Signatures Intelligence – MASINT).
Determining optical signatures of targets is one of the most important tasks of this department, and special attention, judging by the publication [8], is paid to collecting information on spectral optical signatures (features) of targets.
The US Army has systems designed for this purpose, SYERS (Senior Year Electrooptical Reconnaissance System), operating on board the U-2 aircraft in seven spectral ranges, and Cobra Brass, which is a multispectral image sensor for a space-based infrared system.
A lot of attention in the US is paid to the development of multispectral OES with a very large number of spectral windows.
For example, TRW has developed a system with 384 spectral operating ranges.
Such systems have been tested on board unmanned reconnaissance aircraft designed to detect tanks, missile launchers, and other camouflaged military objects located against a “colorful background.”
The use of working spectral ranges in the ultraviolet region of the spectrum will allow identifying the type of enemy missiles by the spectral composition of the radiation of rocket fuel components.
The above is especially characteristic of military and other field systems and complexes.
Nevertheless, attempts to bring the OES of the near future closer to the level of truly intelligent systems do not cease, and a number of results obtained to date are quite optimistic.
The combination of optical-electronic systems with radio-electronic, chemical, acoustic and other means in the presence of new computing means with a very high speed of processing multidimensional information received from these systems allows in real time to quite reliably solve the problems of detection, recognition, classification and identification of a wide variety of objects, i.e. to solve these problems in the interests of tactical units of the ground army, aviation, navy.
Literature.
1. Levshin V.L. Biocybernetic optical-electronic devices for automatic image recognition. — M.: Mashinostroenie, 1987.
2. Krasilnikov N.N., Shelepin Yu.E., Krasilnikova O.I. Mathematical model of color constancy of the human visual system. Optical Journal, 2002, v. 69, no. 5, pp. 38 — 44.
3. Remote sensing: a quantitative approach/Sh.M.Davis, D.A.Landgrebe, T.L.Phillips et al. Ed. F.Swain and Sh.Davis. Translated from English. — M.: Nedra, 1983.
4. Yakushenkov Yu.G. Theory and calculation of optical-electronic devices. 4th ed., revised and enlarged. – M.: Logos, 1999.
5. Miroshnikov M.M. Theoretical foundations of optical-electronic devices. 2nd ed., revised and enlarged. – L.: Mashinostroenie, 1983.
6. McAulay A., Kadar I. Neural networks for adaptive shape tracking.- SPIE Proc., vol.1408 (1991), pp.l19 – 134.
7. MIX and match for better vision/L.A.Chan, A.Colberg, S.Der et al. – SPIE’s OE Magazine, April 2002, pp.18 – 20.
8. Journal of Electronic Defense. – 1998, № 8, pp.p. 43 – 48.

Добавить комментарий