Different units — different results of measuring the sensitivity of television cameras..
KRUTIK Mikhail Ilyich,
MAYOROV Viktor Petrovich
LUMENS, CANDELAS, WATTS AND PHOTONS. DIFFERENT UNITS – DIFFERENT RESULTS OF MEASURING THE SENSITIVITY OF TV CAMERAS BASED ON IMAGE TUBE AND CCD
The authors of this article, due to the nature of their work, very often encounter some confusion in the minds of our partners and customers regarding the sensitivity of CCD cameras.
The article discusses a method for assessing the sensitivity of television systems (including pulsed ones) using energy units of optical radiation (joule, watts, photon). According to the authors, this method is quite universal when recording images and is applicable across the entire optical radiation spectrum. In contrast, the calculation method based on lighting units (candela, lumen, lux) is strictly applicable only within the visible range. Some examples of energy calculations are given, which will help the reader to see for himself the simplicity of the method and the unambiguity of the results obtained.
Of the many existing television systems, the article considers only CCD cameras, including those with preliminary image amplification stages on image converters (EC). The method under consideration may be applicable both to the standard television mode (continuous accumulation mode) and to the pulse mode (including single-shot).
So that when reading the subsequent material there are no questions about the correctness of the provisions used, the main definitions from photometry and radiometry are given below.
The measurement of light quantities is carried out by photometry, and the measurement of radiation in the entire optical range is radiometry. Accordingly, light units are often called photometric, and energy units are called radiometric. The correspondence between photometric and radiometric units is given in Table 1. The subscript e for the corresponding quantities denotes their energy character, and the subscript vphotometric. Of the entire vast area of the optical radiation region (10 nm — 1 mm), only a narrow band of the spectrum from 380 to 780 nm (light radiation) can be perceived by the human eye.
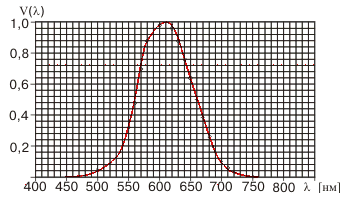
All metrology in the visible spectrum is based on the eye of a standard photometric observer, whose sensitivity to light radiation functionally depends on the wavelength. This function V(l) is called “spectral luminous efficiency” V(l). Its graphical form is shown in Fig. 1, and the tabular form is shown in Table 2 [1].
Table 1. Basic energy and luminous quantities (according to the SI system and the International Illuminating Vocabulary)
Fig. 1. Spectral luminous efficiency
Table 2. Dependence of the relative spectral efficiency on the radiation wavelength
| l , nm | V(l) | l , nm | V(l ) | l , nm | V( l) | l , nm | V(l) |
| 380 | 0.00004 | 480 | 0.139 | 580 | 0.870 | 690 | 0.0082 |
| 390 | 0.00012 | 490 | 0.208 | 590 | 0.757 | 700 | 0.0041 |
| 400 | 0.00040 | 500 | 0.323 | 600 | 0.631 | 710 | 0.0021 |
| 410 | 0.0012 | 510 | 0.503 | 610 | 0.503 | 720 | 0.00105 |
| 420 | 0.0040 | 520 | 0.710 | 620 | 0.381 | 730 | 0.00052 |
| 430 | 0.0116 | 530 | 0.862 | 630 | 0.265 | 740 | 0.00025 |
| 440 | 0.023 | 540 | 0.954 | 640 | 0.175 | 750 | 0.00012 |
| 450 | 0.038 | 550 | 0.995 | 650 | 0.107 | 760 | 0.00006 |
| 460 | 0.060 | 555 | 1.0000 | 660 | 0.061 | 770 | 0.00003 |
| 470 | 0.091 | 560 | 0.995 | 670 | 0.032 | ||
| 570 | 0.952 | 680 | 0.017 |
l wavelength of radiation in nanometers;
V(l) values of relative spectral efficiency at a given value l
Historically, the metrology of light measurements developed first. It was the eye that was the standard radiation receiver for over 200 years, on the basis of which all assessments and measurements of luminous intensity, brightness and illumination were carried out. Subsequently, a device for measuring illumination (luxmeter) was created, which has a spectral characteristic that coincides with the spectral characteristic of the eye of a standard observer.
Television cameras with CCD matrices and image intensifiers have spectral characteristics that differ significantly from the spectral efficiency of the eye. Their range can extend from ultraviolet (120 nm for image intensifiers) to infrared (1 μm for image intensifiers and CCDs). The use of these devices in conditions where radiation of a wider spectrum than visible enters their input leads to the fact that the readings of the lux meter (measuring radiation only in the visible range) carry practically no reliable information. The article will provide a calculation that shows that for a 1/2″ CCD camera matrix, the advertised illumination of 0.0003 lux corresponds to an energy exposure per cell of this matrix of less than 1 photon.
To qualitatively explain such errors, let us consider an example of using a low-level television camera with an image amplification stage on an image intensifier tube with a gallium arsenide photocathode in night conditions.
Figure 2 shows the relative spectral characteristics of:
- the radiation of the night vault (curve 3) [2];
- the sensitivity of the gallium arsenide photocathode of the image intensifier tube (curve 2);
- the sensitivity of the human eye and the corresponding sensitivity of the device measuring illumination – a luxmeter (curve 1);
- sensitivity of the ICX249 CCD matrix from SONY (curve 4).

Fig. 2. Relative spectral characteristics:
of various photoelectronic receivers (1, 2, 4);
of the radiation of the moonless night sky (3).
The graphs show that under moonless night conditions the infrared radiation power of the night vault (l і 760 nm) significantly exceeds its radiation power in the visible range. The luxmeter measures only the visible, very small part of the entire radiation flux. It is concentrated in the range of 400 – 700 nm. In contrast, the photocathode of the image intensifier tube senses optical radiation in the range of 500 – 900 nm and “works” with a larger flux. Similar conclusions are obtained when using a CCD television camera in the same conditions, the silicon crystal of which also has good sensitivity in the infrared range up to 1 µm (curve 4).
From all of the above, we can conclude that for television systems with spectral characteristics different from the spectral sensitivity of the eye, the use of lighting units (lux, lumen, etc.) is not entirely correct (correct, but not entirely or completely incorrect — the choice is up to the reader).
The method of assessing and calculating the sensitivity of television systems in energy units (watt, joule, number of photons) is free from the above-mentioned shortcomings.
Here are the main definitions and constants.
The definition of candela, adopted in 1948 and valid until 1979, was as follows:
Candela is the intensity of light emitted in a perpendicular direction by 1/600,000 m2 of the surface of a black body at the freezing temperature of platinum (2042 K) and a pressure of 101,325 N/m2.
Various experiments yielded results that showed that at a wavelength of l = 555 nm, radiation of 1 W corresponds to a luminous flux of 676 — 688 lm. This ratio already made it possible to convert lumens to watts and back, although opponents still had doubts about the correctness of the method used. In 1979, at the 16th General Conference on Weights and Measures, a new definition of the candela was adopted [3].
The candela is the luminous intensity in a given direction from a source of monochromatic radiation of frequency 540 x 1012 Hz and having a radiant intensity in that direction equal to 1/683 W in a solid angle of one steradian.
A radiation frequency of 540 x 1012 Hz corresponds to a wavelength of λ = 555.016 nm in air under standard conditions, which for almost all purposes may be taken to be equal to 555 nm without affecting the accuracy of actual measurements.
Based on this fundamental definition, photometric units can be unambiguously converted into radiometric units and vice versa.
One more (and last) thing we need is a formula for calculating the quantum energy. The fact is that in many cases it is more convenient to calculate the energy not in integral quantities (watt, joule and their derivatives), but in the number of photons (per unit of time, per unit of area, etc.). In particular, many developers of CCD cameras and qualified users already estimate their sensitivity by the number of electrons in the cell (in other words, by the number of quanta). Therefore, it is of particular interest to calculate the entire photoelectronic complex (input lens + image intensifier + projection lens + CCD camera) based on the quantum nature of light. Moreover, such calculation is very convenient in the pulsed mode of irradiation of the recorded image (including single irradiation).
The energy of a radiation quantum (photon) is calculated using the well-known formula:
Q = (h * c) /l , (1)
where c – the speed of light in a vacuum (2.998×108 m/s);
h – Planck's constant (6.6262×10-34 J*s);
l is the wavelength of radiation (m).
The energy of a quantum of radiation at l1 = 555 nm is respectively equal to:
Q (l1) = 3.58 x 10-19 J (2)
The reciprocal value corresponds to the number of quanta per second in radiation with a power of 1 W at l1 = 555 nm:
Nph [1W] (l1) = 1/Q (l1) = 1/3.58 x 10-19 = 2.79 x 1018 ph/s (3)
The subscript ph means that we are talking about photon quantities.
From the definition of candela it follows that at l1 = 555 nm
Nph [1W] (l1) = 683 lm.(4)
Therefore, we can obtain the exact value of the number of photons at l1 = 555 nm per second in a luminous flux equal to 1/683 W, which at this wavelength corresponds to a luminous flux of 1 lm:
Nph [1 lm] (l1) = Nph [1 W] (l1)/683 = 0.409 x 1016 phot/s (5)
Using the definition of the unit of illumination, we find that at l1 = 555 nm the number of photons falling in 1 second on a surface of 1 m2 with an illumination of 1 lx is equal to:
Nph [1 lx] = Nph [1 lm]/m2 = 0.409 x 1016 ph /(s*m2) (6)
Now it can be shown why the use of lighting units (lumens, lux, etc.) in calculating the sensitivity of television systems often gives erroneous results.
For this purpose, a comparative calculation of the average number of electrons in a CCD matrix cell is given when it is irradiated with the same power at two different wavelengths: l1 = 555 nm and l2 = 630 nm. The luxmeter readings will be a clear demonstration of the assertion being proven. As indicated above, its relative spectral characteristic is similar to the relative spectral luminous efficiency of the eye of a standard photometric observer (Fig. 1, Table 2).
To simplify calculations, the radiation flux Фе1 is taken to be equal to:
Фе1 = 1/683 W.
At l1 = 555 nm, such a radiation flux corresponds to a luminous flux
Фv1 = 1 lm.
Provided that the given flux falls on an area of 1 m2, the irradiance of the CCD matrix surface will be
Ee1 = (1/683) W/m2 ,
which corresponds to an illumination of
Ev1 = 1 lx.
This illumination value at l1 = 555 nm will be shown by the lux meter.
Now the average number of electrons generated in a CCD matrix cell when irradiated with a given flux is calculated. The CCD matrix from SONY ICX249 is taken as an example. This is a 1/2-inch matrix with the following characteristics:
| H*V – size of the active part of the crystal |
6.47 x 4.83 mm; |
| P – number of active pixels | 752 x 582; |
| h*v – pixel size | 8.6 x 8.3 μm; |
| relative spectral characteristic | (Fig. 2, curve 4); |
| h1 is the matrix quantum efficiency (at l1 ~555 nm) | ~0.6; |
| h2 is the matrix quantum efficiency (at l2 ~630 nm) | ~0.7; |
| t н is the accumulation time. | 20 ms |
From the above calculations (formulas (1) — (6)) we obtained that at l1 = 555 nm the irradiance Ee1 corresponds to the surface photon density
Nph1( l1) = 0.409 x 1016 photons /(s*m2)]
From the calculated matrix pixel area:
Spix = 8.6 x 8.3 x 10-12 = 7.14 x 10-11 m2, (7)
and the specified accumulation time t н = 20 ms, the number of photons (at l1 = 555 nm) falling on the matrix pixel during the specified time is determined:
Nph1-pix(l1) = Nph1(l1) x Spix x t n = 5.84 x 103 ph
The quantum efficiency of the ICX249 matrix at l1 = 555 nm is approximately equal to 0.6 (Fig. 2, curve 4).
Thus, at an irradiance l1 = 555 nm of the CCD matrix surface equal to Ee1 = (1/683) W/m2, the average number of electrons accumulated in one pixel for t n = 20 ms, is equal to
N[el]1-pix = Nph1-pix (l1) x 0.6 = 3.36 x 103 el,(8)
where the subscript [el] means that we are talking about the number of electrons.
Now we calculate the average number of electrons in the cell at the same irradiance of 1/683 W/m2, but at l2 = 630 nm.
From (1) we find the quantum energy:
Q (l2) = 3.15 x 10-19 J (9)
The number of photons in a flux with a power of 1 W in 1 second at l 2 = 630 nm is respectively equal to
Nph[1W] (l2) = 1/Q (l2) = 3.17 x 1018 photons/s, (10)
and in a flux with a power of 1/683 W respectively
Nph [1/683 W] (l2) = (3.17? 1018)/683 = 0.46 x 1016 photons/s. (11)
Provided that this flux falls on an area equal to 1 m2, the corresponding photon density (photon irradiance) is
Nph2(l2) = 0.46 x 1016 ph /(s*m2) (13)
Multiplying the obtained value by the area of the Spix matrix cell (7) and the accumulation time t н, we find the number of photons (at l = 630 nm) falling on the pixel during the specified time
Nph2-pix( l2) = Nph2( l2) x Spix x t н =6.625 x 103 ph (14)
The quantum efficiency of the ICX249 matrix at l = 630 nm is approximately 0.7 (Fig. 2, curve 4). As a result, we find that the average number of electrons accumulated in one cell in 20 ms is
N[el]2-pix = Nph2-pix (l 2) x 0.7 = 4.64 x 103 el. (15)
It should be recalled that at a wavelength of l = 555 nm, the energy irradiance of 1/683 W corresponds to an illumination of 1 lx, and at a wavelength of l = 630 nm, the same irradiance corresponds to an illumination of 0.265 lx. This follows from the spectral luminous efficiency (Fig. 1, Table 2).
Thus, in energy units (W), the sensitivity of the ICX249 matrix at a wavelength of l = 630 nm is approximately 1.4 times greater than at l = 555 nm. But in light units (lx), at the same wavelength, its sensitivity is already 5.3 times greater (in parrots, the boa constrictor turned out to be significantly longer).
Let us summarize the obtained results (formulas (6), (8), (13) and (15)) in Table 3. At an illumination on the matrix surface equal to 10-2 lx (l = 555 nm), a signal charge equal to 35 electrons is formed in each pixel. In this case, what can the sensitivity of 0.0003 lx specified by the manufacturer mean for the WAT-902H CCD camera, in which the ICX249 matrix is installed? At such illumination, during the accumulation time of 20 ms, an average of 1 2 photons arrive at the cell, which gives an average of less than 1 electron per pixel.
Table 3 shows that to form a signal in the CCD matrix equal to the intrinsic noise level of electrons in the cells, the illumination on its surface must be at least 10-2 lux.
The fact that many CCD cameras are advertised for operation at significantly lower illumination levels only speaks of their good sensitivity in the infrared region. But this has nothing to do with lux.
The presented method for estimating the energy sensitivity of photodetectors is given only for monochromatic radiation. Estimating the sensitivity of a CCD or image intensifier tube when working with non-monochromatic radiation sources requires mandatory knowledge of both the spectral characteristics of the photodetectors and the spectral composition of the radiation. The calculation is a kind of convolution of these two functions. In practice, such a convolution is most often performed graphically. Dividing the entire spectral range into intervals within which the value of the source radiation power and the photodetector quantum efficiency can be considered constant with an acceptable error, the calculation is performed for each of the intervals. Then the obtained results are summed up.
Table 3. Calculation results
Literature
1. M.I. Epshteyn. Measurements of optical radiation in electronics. «Energy», 1975.
2. V.A. Orlov, V.I. Petrov. Night vision devices with limited visibility. Moscow Military Publishing House, 1989.
3. NIST Special Publication SP330 «The International System of Units (SI).» The US edition of the above BIPM publication.

Добавить комментарий