 |
Эпименид Кносский с острова Крит – полумифический поэт и философ, живший в VI в. до н.э., однажды заявил: «Все критяне – лжецы!». Так как он и сам был критянином, то его помнят как изобретателя так называемого критского парадокса.
В терминах аристотелевой логики, в которой утверждение не может быть одновременно истинным и ложным, и подобные самоотрицания не имеют смысла. Если они истинны, то они ложны, но если они ложны, то они истинны.
И здесь на сцену выходит нечеткая логика, где переменные могут быть частичными членами множеств. Истинность или ложность перестают быть абсолютными – утверждения могут быть частично истинными и частично ложными. Использование подобного подхода позволяет строго математически доказать, что парадокс Эпименида ровно на 50% истинен и на 50% ложен.
Таким образом, нечеткая логика в самой своей основе несовместима с аристотелевой логикой, особенно в отношении закона Tertium non datur («Третьего не дано» – лат.), который также называют законом исключения среднего1. Если сформулировать его кратко, то звучит он так: если утверждение не является истинным, то оно является ложным. Эти постулаты настолько базовые, что их часто просто принимают на веру.
Более банальный пример пользы нечеткой логики можно привести в контексте концепции холода. Большинство людей способно ответить на вопрос: «Холодно ли вам сейчас?». В большинстве случаев (если вы разговариваете не с аспирантом-физиком) люди понимают, что речь не идет об абсолютной температуре по шкале Кельвина. Хотя температуру в 0 oK можно, без сомнения, назвать холодом, но температуру в +15 oC многие холодом считать не будут.
Но машины не способны проводить такую тонкую градацию. Если стандартом определения холода будет «температура ниже +15 oC», то +14,99 oC будет расцениваться как холод, а +15 oC – не будет.
Теория нечетких множеств
Хотя нечеткая логика обычно изучается лишь на старших курсах вузов, ее базовые концепции удивительно просты.
Рассмотрим рис. 1. На нем представлен график, помогающий понять то, как человек воспринимает температуру. Температуру в +60 oF (+12 oC) человек воспринимает как холод, а температуру в +80 oF (+27 oC) – как жару. Температура в +65 oF (+15 oC) одним кажется низкой, другим – достаточно комфортной. Мы называем эту группу определений функцией принадлежности к множествам, описывающим субъективное восприятие температуры человеком.
Так же просто можно создать дополнительные множества, описывающие восприятие температуры человеком. Например, можно добавить такие множества, как «очень холодно» и «очень жарко». Можно описать подобные функции для других концепций, например, для состояний «открыто» и «закрыто», температуры в охладителе или температуры в башенном охладителе.
То есть нечеткие системы можно использовать как универсальный аппроксиматор (усреднитель) очень широкого класса линейных и нелинейных систем. Это не только делает более надежными стратегии контроля в нелинейных случаях, но и позволяет использовать оценки специалистов-экспертов для построения схем компьютерной логики.
Нечеткие операторы
Чтобы применить алгебру для работы с нечеткими значениями, нужно определить используемых операторов. Обычно в булевой логике используется лишь ограниченный набор операторов, с помощью которых и производится выполнение других операций: NOT (оператор «НЕ»), AND (оператор «И») и OR (оператор «ИЛИ»).
Можно дать множество определений для этих трех базовых операторов, три из которых приведены в таблице. Кстати, все определения одинаково справедливы для булевой логики (для проверки просто подставьте в них 0 и 1).
В булевой логике значение FALSE («ЛОЖЬ») эквивалентно значению «0», а значение TRUE («ИСТИНА») эквивалентно значению «1». Аналогичным образом в нечеткой логике степень истинности может меняться в диапазоне от 0 до 1, поэтому значение «Холод» верно в степени 0,1, а операция NOT(«Холод») даст значение 0,9.
Вы можете вернуться к парадоксу Эпименида и постараться его решить (математически он выражается как A = NOT(A), где A – это степень истинности соответствующего утверждения). Если же вы хотите более сложную задачу, то попробуйте решить вопрос о звуке хлопка, производимого одной рукой…
Решение задач методами нечеткой логики
Лишь немногие клапаны способны открываться «чуть-чуть». При работе оборудования обычно используются четкие значения (например, в случае бимодального сигнала 0-10 В), которые можно получить, используя так называемое «решение задач методами нечеткой логики». Подобный подход позволяет преобразовать семантические знания, содержащиеся в нечеткой системе, в реализуемую стратегию управления.
Это можно сделать с использованием различных методик, но для иллюстрации процесса в целом рассмотрим всего один пример.
В методе height defuzzification результатом является сумма пиков нечетких множеств, рассчитываемая с использованием весовых коэффициентов. У этого метода есть несколько недостатков, включая плохую работу с несимметричными функциями принадлежности к множествам, но у него есть одно преимущество – этот метод наиболее простой для понимания.
Предположим, что набор правил, управляющих открытием клапана, даст нам следующий результат:
«Клапан закрыт»: 0,1
«Клапан частично закрыт»: 0,2
«Клапан частично открыт»: 0,7
«Клапан открыт»: 0,3
Если мы используем метод height defuzzification для определения степени открытости клапана, то получим результат:
(0,1*0% + 0,2*25% + 0,7*75% + 0,3*100%)//(0,1 + 0,2 + 0,7 + 0,3) = (0% + 5% + 52,5% + 30%)/(1,3) = 87,5/1,3 = 67,3%,
т.е. клапан необходимо открыть на 67,3%.
Практическое применение нечеткой логики
Когда только появилась теория нечеткой логики, в научных журналах можно было найти статьи, посвященные ее возможным областям применения. По мере продвижения разработок в данной области число практических применений для нечеткой логики начало быстро расти. В настоящее время этот список был бы слишком длинным, но вот несколько примеров, которые помогут понять, насколько широко нечеткая логика используется в системах управления и в экспертных системах.
– Устройства для автоматического поддержания скорости движения автомобиля и увеличения эффективности/стабильности работы автомобильных двигателей (компании Nissan, Subaru).
– Системы распознавания рукописного текста в PDA (компания Sony).
– Улучшение систем безопасности для атомных реакторов (компании Hitachi, Bernard, Nuclear Fuel Div.).
– Управление роботами (компании Toshiba, Fuji Electric, Omron).
– Промышленные системы управления (компании Aptronix, Omron, Meiden, Sha, Micom, Nisshin-Denki, Mitsubishi, Oku-Electronics и др.).
Чтобы показать, где нечеткая логика используется в системах автоматизации, приведу несколько правил, которые позволяют увеличить эффективность работы коммунальных систем в зданиях или могут способствовать выявлению неисправностей. Выделены параметры, являющиеся нечеткими значениями.
Нечеткая логика в системах автоматизации зданий
Хотя использование нечеткой логики может действительно стать следующим шагом в создании систем автоматического управления коммунальными системами в зданиях (building automation systems/BAS), важно помнить, что для осмысленного применения нечеткой логики необходимо, чтобы программное обеспечение, управляющее работой BAS, с самого начало создавалось с учетом возможности использования этих функций. Недостаточен только лишь условный язык, используемый для задания правил, его интегрированность в програм-мное обеспечение и соответствие принципам его работы. Еще нужно установить четкое разграничение между стандартными ресурсами и способами управления (например, ПИД-регулированием, использованием расписаний, предупреждающих сообщений и т.д.) и методами управления на основе нечеткой логики. Неполная интеграция или неправильно построенные правила взаимопреобразований между стандартной и нечеткой логикой могут привести к появлению в программах ошибок, причину которых будет очень сложно установить.
Кроме того, большая часть информации, необходимой для эффективной работы систем, основанных на методах нечеткой логики, должна автоматически собираться во время первоначального запуска программного обеспечения, управляющего работой системы. Если возложить программирование системы на инженеров-строителей, то это будет неосмотрительным со стороны разработчиков BAS и приведет к тому, что в большинстве зданий BAS не будут использоваться надлежащим образом. Например, необходимо задать функции принадлежности к множествам (см. рис. 1 и 2) для величин, часто используемых в BAS. Если добавить датчики температуры воздуха или контроллеры для систем кондиционирования с переменным расходом воздуха, то компьютерная программа должна быть способной автоматически задавать соответствующие функции принадлежности к множествам для различных контрольных точек.
Так как цены на энергоносители непрерывно растут и становится очевидным, что необходимо использование передовых систем для обнаружения неисправностей, то проектировщики зданий и управляющие компании должны отслеживать возможности по использованию инновационных решений. «Нечеткая логика» – это термин, который у всех на слуху, и при правильном использовании этот метод вполне может оправдать возлагаемые на него надежды.
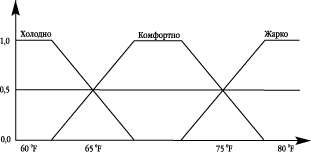
Рис. 1. Нечеткое определение температуры
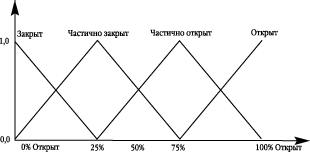
Рис. 2. Описание работы нечеткого клапана
Парадокс Эпименида
В наиболее упрощенной форме парадокс Эпименида можно выразить в следующей форме: «Это предложение ложно». Если выразить его в алгебраических терминах, то он будет выглядеть следующим образом:
A = NOT(A).
Таким образом, если ограничиваться понятиями булевой логики, то это уравнение принимает парадоксальный вид:
0 = 1.
Однако при использовании нечеткой логики это уравнение можно решить следующим образом:
A = NOT(A)
A = 1— A
2A = 1
A = 0,5.
Таким образом, предложение из парадокса Эпименида оказывается ровно на 50% истинным и на 50% – ложным.
Распространенные ложные представления о нечеткой логике
Нечеткая логика является неточной: по своей основе нечеткая логика не более неточна, чем стандартная арифметика. Фактически она гораздо более точна при работе с неточной информацией.
В основе нечеткой логики лежат вероятностные рассуждения. Вероятность имеет дело с шансами возникновения тех или иных событий, а нечеткая логика – с самими этими событиями. Обычно нечеткая логика имеет дело с двусмысленностью,
а не с неопределен-ностью.
Нечеткая логика построена на основе ряда эвристических предположений.
Хотя из-за интуитивной природы нечеткой логики с первого взгляда и может показаться, что лежащие в ее основе правила выбраны произвольно или основаны только на здравом смысле, но в действительности было строго доказано, что эти правила являются верными.
Лотфи Заде, отец нечеткой логики
Доктор Лотфи Заде, родившийся в 1921 году, считается отцом-основателем использования нечеткой логики. Закончив в 1942 году Тегеранский университет и получив степень по электротехнике, он уехал в США, где обучался в Массачусетском технологическом институте (1946 г.) и в Колумбийском университете (1949 г.), где позднее преподавал теорию систем.
Его основополагающая статья по нечеткой логике была опубликована в 1965 г. и получила не слишком-то теплый прием со стороны некоторых кругов академического сообщества. Даже сейчас, сорок лет спустя, в этой области все еще остаются некоторые разногласия, но методы нечеткой логики стали одним из инструментов, используемым инженерами при проектировании измерительно-контрольных систем.
И хотя доктор Лотфи Заде известен в основном как разработчик принципов нечеткой логики, он также был одним из пионеров в области разработки Z-преобразования для получения дискретных сигналов и в системном анализе, с которыми должны быть знакомы все, кто интересуется проблемами использования микроконтроллеров для обработки цифровых сигналов и осуществления функций цифрового управления.
[1] Два других закона аристотелевой логики также опровергаются нечеткой логикой: это закон идентичности, утверждающий: «если утверждение истинно, то оно верно»; и закон противоречия: «утверждение не может быть одновременно истинным и ложным».
[2] В качестве алгоритма, базирующегося на нечеткой логике, результаты которого обычно превосходят результаты использования ПИД-регулирования, можно привести контроллер Мамдани:
http://esru.strath.ac.uk/Reference/concepts/fuzzy/fuzzy.htm
[3] Более полный список можно найти по следующему адресу:
http://esru.strath.ac.uk/Reference/concepts/fuzzy/fuzzy_appl.10.htm
Энвер Баши
старший инженер-исследователь компании Computrols, Inc.
По материалам сайта AutomatedBuildings
|
|